巖土工程中的準與不準

楊光華

（廣東省水利水電科學研究院）  轉載于巖土網

巖土工程要做到精確是困難的，但安全則是必須的。這可能就是太沙基所說的土力學是一門藝術的一種含義吧！

土力學中地基的沉降計算中應力分布是依據連續體彈性力學計算的，土應該是介于連續與非連續的介質，所以這其中的計算理論就存在差異，同時，巖土體是天然介質，其分布也是非均勻的，而理論計算是假設均勻分布的，至少對于同層土是均勻分布的，其實對于同一層土，由于自重或風化的作用，不同深度位置也是有差異的，因此，要描述自然巖土的非均勻性也是比較困難的，這也導致土的參數的差異性的存在。眾多的不確定性，這就注定在有限科學條件下，這門學科的非精確性。

但工程建設必須要安全可靠，因此要在安全前提下提高準確性、科學性。

以p-s曲線方法解決地基承載力問題為例，探討巖土工程的準與不準。

楊光華等提出用實際基礎的荷載沉降的p-s曲線^[1、2]，按強度和變形雙控確定地基的允許承載力，如圖1，p-s曲線由切線模量法^[3]計算得到。切線模量法由現場壓板載荷試驗曲線建立，如圖2，假設壓板載荷試驗的p-s曲線符合雙曲線，用曲線的初始斜率k₀，按彈性力學公式反算土的初始切線模量E_t0，取壓板試驗的最大荷載p_max作為極限荷載反計算地基的強度參數c,φ 。用壓板試驗反算得到的參數，由切線模量法計算得到實際基礎的p-s曲線見圖1，實際基礎的極限承載力由壓板試驗反算的c,φ，按相同的模型計算得到。

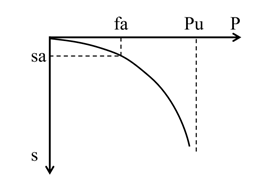
圖1 確定地基承載力的p~s曲線

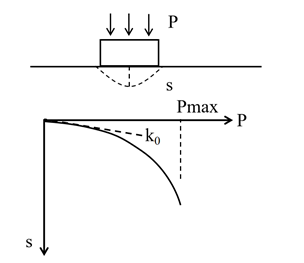
圖2 壓板載荷試驗曲線

    由圖1，地基的允許承載力f_a由地基強度安全和變形控制雙控確定：

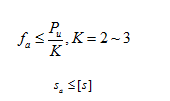
K為地基承載力安全系數，[s]為允許的基礎沉降。

顯然，這里存在不確定的特性：

1、極限承載力的誤差

2、雙曲線方程假設的誤差

3、按彈性力學計算的誤差

但這些誤差不影響安全，在安全保證方面有足夠的準確性：

1、強度安全，即使極限承載力有誤差，但有安全系數K=2~3的保證，更有計算極限承載力的土體強度參數是利用壓板載荷試驗的最大荷載控制，這個荷載值是小于實際極限承載力的，因此，強度安全的準確性是可保證的。

2、沉降的準確性，因允許承載力f_a對應安全系數較大，理論上對應的沉降接近于線性段，而線性段沉降的準確性取決于曲線的初始切線模量k₀，而這個初始模量是由現場原位壓板試驗反算的土的初始切線模量E_t0計算的，具有較高的可靠性，從而保證了實際基礎沉降的準確性。

3、計算模型的可靠性，切線模量法的參數是由壓板試驗反算的，其計算所用模型是與實際基礎用相同的模型，參數與計算模型是配套的，從而保證計算模型的可靠性。

因此，用這種方法計算的基礎沉降或地基的承載力，即使在一些計算假設上存在不準確性，包括上面提到的一些客觀上的不準確性，但實際上，即使極限承載力不準確，由于有安全系數做保障，強度安全是足夠可靠的，變形計算由于土的初始模量是現場反算的，反算模型和實際基礎計算模型相同，可以保證其可靠性，對于工程設計有足夠的準確性，這個方法應該比目前一些經驗系數法有更好的準確性。這是一個比較巧妙的方法，也是體現太沙基關于巖土工程的科學性與藝術性的方法。因此，巖土工程的不準確性是客觀存在的，而保證安全性是必須的，提高準確性是發展的目標。

[1] 楊光華.確定地基承載力的p-s曲線法[J].地基處理,2022,4(02):91-98.

[2]楊光華,姜燕,張玉成,王恩麒.確定地基承載力的新方法[J].巖土工程學報,2014,36(04):597-603.

[3]楊光華.地基非線性沉降計算的原狀土切線模量法[J].巖土工程學報,2006(11):1927-1931.